Tutorial PyTorch: um guia rápido para você entender agora os fundamentos do PyTorch

O Python está bem estabelecido como a linguagem ideal para ciência de dados e aprendizado de máquina, e isso se deve em parte à biblioteca de ML de código aberto PyTorch.

A combinação do PyTorch com ferramentas poderosas de construção de rede neural profunda e fáceis de uso, torna-o uma escolha popular entre cientistas de dados. À medida que sua popularidade cresce, mais e mais empresas estão mudando do TensorFlow para o PyTorch, tornando-se agora o melhor momento para começar a usar o PyTorch.

Hoje, vamos te ajudar a entender o que torna o PyTorch tão popular, alguns fundamentos do uso dessa biblioteca e ajudá-lo a fazer seus primeiros modelos computacionais.

O que é o PyTorch?

O PyTorch é uma biblioteca Python de aprendizado de máquina de código aberto usada para implementações de aprendizado profundo, como visão computacional (usando TorchVision) e processamento de linguagem natural. Essa biblioteca foi desenvolvida pelo laboratório de pesquisa de IA do Facebook (FAIR) em 2016 e, desde então, é adotada nos campos da ciência de dados e ML.

O PyTorch torna o aprendizado de máquina intuitivo para aqueles que já estão familiarizados com Python e tem ótimos recursos como suporte OOP e gráficos de computação dinâmica.

Junto com a construção de redes neurais profundas, o PyTorch também é ótimo para cálculos matemáticos complexos por causa de sua aceleração de GPU. Esse recurso permite que o PyTorch use a GPU do seu computador para acelerar enormemente os cálculos.

Essa combinação de recursos exclusivos e a simplicidade incomparável do PyTorch o torna uma das bibliotecas de aprendizado profundo mais populares, competindo apenas com o TensorFlow pelo primeiro lugar.

Por que usar o PyTorch?

Antes do PyTorch, os desenvolvedores usavam cálculos avançados para encontrar as relações entre erros retro-propagados e peso do nó. Redes neurais mais profundas exigiam operações cada vez mais complicadas, o que restringia o aprendizado de máquina em escala e acessibilidade.

Agora, podemos usar bibliotecas de ML para completar automaticamente todo esse cálculo! As bibliotecas de ML podem computar redes de qualquer tamanho ou formato em questão de segundos, permitindo que mais desenvolvedores criem redes maiores e melhores.

O PyTorch leva essa acessibilidade um passo adiante, comportando-se como o Python padrão. Em vez de aprender uma nova sintaxe, você pode usar o conhecimento existente de Python para começar rapidamente. Além disso, você pode usar bibliotecas Python adicionais com PyTorch, como depuradores populares como o PyCharm.

PyTorch vs. TensorFlow

A principal diferença entre PyTorch e TensorFlow é a escolha entre simplicidade e desempenho: o PyTorch é mais fácil de aprender (especialmente para programadores Python), enquanto o TensorFlow tem uma curva de aprendizado, mas tem um desempenho melhor e é mais usado.

• Popularidade: Atualmente, o TensorFlow é a ferramenta ideal para profissionais e pesquisadores do setor porque foi lançado 1 ano antes do PyTorch. No entanto, a taxa de usuários do PyTorch está crescendo mais rápido do que a do TensorFlow, sugerindo que o PyTorch pode em breve ser o mais popular.

• Paralelismo de dados: O PyTorch inclui paralelismo de dados declarativo, em outras palavras, ele distribui automaticamente a carga de trabalho do processamento de dados em diferentes GPUs para acelerar o desempenho. O TensorFlow tem paralelismo, mas exige que você atribua o trabalho manualmente, o que costuma ser demorado e menos eficiente.

• Gráficos dinâmicos vs. estáticos: PyTorch tem gráficos dinâmicos por padrão que respondem a novos dados imediatamente. O TensorFlow tem suporte limitado para gráficos dinâmicos usando o TensorFlow Fold, mas usa principalmente gráficos estáticos.

• Integrações: PyTorch é bom para usar em projetos na AWS por causa de sua estreita conexão por meio do TorchServe. O TensorFlow está bem integrado com o Google Cloud e é adequado para aplicativos móveis devido ao uso da API Swift.

• Visualização: O TensorFlow tem ferramentas de visualização mais robustas e oferece um controle mais preciso sobre as configurações do gráfico. A ferramenta de visualização Visdom da PyTorch ou outras bibliotecas de plotagem padrão, como matplotlib, não são tão completas quanto o TensorFlow, mas são mais fáceis de aprender.

Fundamentos do PyTorch

Tensores

Os tensores PyTorch são variáveis indexadas (arrays) multidimensionais usadas como base para todas as operações avançadas. Ao contrário dos tipos numéricos padrão, os tensores podem ser atribuídos para usar sua CPU ou GPU para acelerar as operações.

Eles são semelhantes a uma matriz NumPy n-dimensional e podem até ser convertidos em uma matriz NumPy em apenas uma única linha.

Tensores vêm em 5 tipos:

• FloatTensor: 32-bit float

• DoubleTensor: 64-bit float

• HalfTensor: 16-bit float

• IntTensor: 32-bit int

• LongTensor: 64-bit int

Como acontece com todos os tipos numéricos, você deseja usar o menor tipo que atenda às suas necessidades para economizar memória. O PyTorch usa  FloatTensor como o tipo padrão para todos os tensores, mas você pode mudar isso usando:

torch.set_default_tensor_type(t)                           

Para inicializar dois FloatTensors:

import torch
# initializing tensors
a = torch.tensor(2)
b = torch.tensor(1)

Os tensores podem ser usados como outros tipos numéricos em operações matemáticas simples.    

# addition
    print(a+b)
    # subtraction
    print(b-a)
    # multiplication
    print(a*b)
    # division
    print(a/b)

Você também pode mover tensores para serem manipulados pela GPU usando cuda.

if torch.cuda.is_available():
x = x.cuda()
y = y.cuda()
x + y

Como tensores são matrizes em PyTorch, você pode definir tensores para representar uma tabela de números:

ones_tensor = torch.ones((2, 2)) # tensor containing all ones
rand_tensor = torch.rand((2, 2)) # tensor containing random values

Aqui, estamos especificando que nosso tensor deve ser um quadrado 2×2. O quadrado é preenchido com todos os 1 ao usar a função ones() ou números aleatórios ao usar a função rand().

Redes neurais

PyTorch é comumente usado para construir redes neurais devido aos seus modelos de classificação excepcionais, como classificação de imagem ou redes neurais convolucionais (CNN).

As redes neurais são camadas de nós de dados conectados e ponderados. Cada camada permite que o modelo identifique a qual classificação os dados de entrada correspondem.

As redes neurais são tão boas quanto seu treinamento e, portanto, precisam de grandes conjuntos de dados e estruturas GAN, que geram dados de treinamento mais desafiadores com base naqueles já dominados pelo modelo.

O PyTorch define redes neurais usando o pacote torch.nn, que contém um conjunto de módulos para representar cada camada de uma rede.

Cada módulo recebe tensores de entrada e calcula os tensores de saída, que trabalham juntos para criar a rede. O pacote torch.nn também define funções de perda que usamos para treinar redes neurais.

As etapas para construir uma rede neural são:

• Construção: Crie camadas de rede neural, configure parâmetros, estabeleça pesos e tendências.
• Propagação direta: Calcule a saída prevista usando seus parâmetros. Meça o erro comparando a saída prevista e a real.

• Retropropagação: Depois de encontrar o erro, tire a derivada da função de erro em termos dos parâmetros de nossa rede neural. A propagação para trás nos permite atualizar nossos parâmetros de peso.

• Otimização iterativa: Minimize erros usando otimizadores que atualizam parâmetros por meio de iteração usando gradiente descendente.

Aqui está um exemplo de uma rede neural em PyTorch:

import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel, 6 output channels, 3x3 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 3)
self.conv2 = nn.Conv2d(6, 16, 3)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 6 * 6, 120) # 6*6 from image dimension
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))

x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features

net = Net()
print(net)

O nn.module designa que esta será uma rede neural e então a definimos com duas camadas conv2d, que realizam uma convolução 2D, e 3 camadas lineares, que realizam transformações lineares.

A seguir, definimos um método direto para descrever como fazer a propagação direta. Não precisamos definir um método de propagação para trás porque PyTorch inclui uma função backwards() por padrão.

Não se preocupe se isso parece confuso agora, depois vamos cobrir implementações mais simples do PyTorch neste tutorial.

Autograd

Autograd é um pacote PyTorch usado para calcular derivadas essenciais para operações de rede neural. Essas derivadas são chamadas de gradientes. Durante uma passagem para frente, o autograd registra todas as operações em um tensor habilitado para gradiente e cria um gráfico acíclico para encontrar a relação entre o tensor e todas as operações. Essa coleção de operações é chamada de diferenciação automática.

As folhas deste gráfico são tensores de entrada e as raízes são tensores de saída. O Autograd calcula o gradiente traçando o gráfico da raiz à folha e multiplicando cada gradiente usando a regra da cadeia.

Depois de calcular o gradiente, o valor da derivada é preenchido automaticamente como um atributo grad do tensor.

import torch
# pytorch tensor
x = torch.tensor(3.5, requires_grad=True)
# y is defined as a function of x

y = (x-1) * (x-2) * (x-3)
# work out gradients
y.backward()

Por padrão, requires_grad é definido como false e o PyTorch não rastreia gradientes. Especificar requires_grad como True durante a inicialização fará o PyTorch rastrear gradientes para este tensor em particular sempre que realizarmos alguma operação nele.

Este código olha para y e vê que ele veio de (x-1) * (x-2) * (x-3) e calcula automaticamente o gradiente dy / dx, 3x^2 – 12x + 11.

A instrução também calcula o valor numérico desse gradiente e o coloca dentro do tensor x ao lado do valor real de x, 3.5.

Juntos, o gradiente é 3 * (3.5 * 3.5) – 12 * (3.5) + 11 = 5.75.

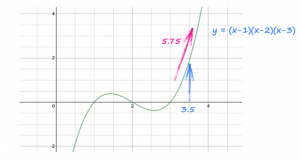
                                                 Figura 01

Os gradientes se acumulam por padrão, o que pode influenciar o resultado se não for redefinido. Use model.zero_grad() para zerar novamente seu gráfico após cada gradiente.

Otimizadores

Os otimizadores permitem que você atualize os pesos e tendências dentro de um modelo para reduzir o erro. Isso permite que você edite como seu modelo funciona sem ter que refazer tudo.

Todos os otimizadores PyTorch estão contidos no pacote torch.optim, com cada esquema de otimização projetado para ser útil em situações específicas. O módulo torch.optim permite que você construa um esquema de otimização abstrato apenas passando uma lista de parâmetros. O PyTorch tem muitos otimizadores para escolher, o que significa que quase sempre há um que melhor se adapta às suas necessidades.

Por exemplo, podemos implementar o algoritmo de otimização comum, SGD (Stochastic Gradient Descent), para suavizar nossos dados.

import torch.optim as optim
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-3
## SGD
optimizer = optim.SGD([params], lr=learning_rate)

Depois de atualizar o modelo, use optimizer.step() para dizer ao PyTorch para recalcular o modelo.

Sem usar otimizadores, precisaríamos atualizar manualmente os parâmetros do modelo, um por um, usando um loop:

for params in model.parameters():
params -= params.grad * learning_rate

No geral, os otimizadores economizam muito tempo, permitindo que você otimize a ponderação dos dados e altere o modelo sem refazê-lo.

Gráficos de computação com PyTorch

Para entender melhor o PyTorch e as redes neurais, é importante praticar com gráficos de computação. Esses gráficos são essencialmente uma versão simplificada de redes neurais com uma sequência de operações usadas para ver como a saída de um sistema é afetada pela entrada.

Em outras palavras, a entrada x é usada para encontrar y, que então é usada para encontrar a saída z.

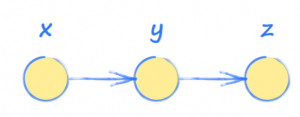
                                                            Figura 02

Imagine que  y e z são calculados assim:

y = x^2

z = 2y + 3

No entanto, estamos interessados em como a saída z muda com a entrada x, então precisaremos fazer alguns cálculos:

dz/dx = (dz/dy) * (dy/dx)

dz/dx = 2.2x

dz/dx = 4x

Usando isso, podemos ver que a entrada x = 3,5 fará com que z = 14.

Saber definir cada tensor em termos dos outros (y e z em termos de x, z em termos de y, etc.) permite que o PyTorch construa uma imagem de como esses tensores estão conectados.

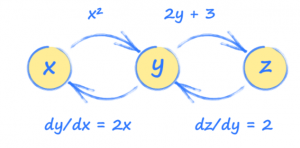
                                                          Figura 03

Esta imagem é chamada de gráfico computacional e pode nos ajudar a entender como o PyTorch funciona nos bastidores.

Usando esse gráfico, podemos ver como cada tensor será afetado por uma mudança em qualquer outro tensor. Esses relacionamentos são gradientes e são usados para atualizar uma rede neural durante o treinamento.

Esses gráficos são muito mais fáceis de fazer usando o PyTorch do que manualmente. Então, agora que entendemos o que está acontecendo nos bastidores, vamos tentar fazer esse gráfico.

import torch
# set up simple graph relating x, y and z
x = torch.tensor(3.5, requires_grad=True)
y = x*x
z = 2*y + 3
print("x: ", x)
print("y = x*x: ", y)
print("z= 2*y + 3: ", z)
# work out gradients
z.backward()
print("Working out gradients dz/dx")

# what is gradient at x = 3.5
print("Gradient at x = 3.5: ", x.grad)

Isso mostra que z = 14, exatamente como encontramos manualmente acima!

Mãos à obra com PyTorch: gráfico computacional de vários caminhos

Agora que você viu um gráfico computacional com um único conjunto relacional, vamos tentar um exemplo mais complexo.

Primeiro, defina dois tensores, a e b, para funcionar como nossas entradas. Certifique-se de definir requires_grad=True para que possamos fazer gradientes na linha.

import torch
# set up simple graph relating x, y and z
a = torch.tensor(3.0, requires_grad=True)
b = torch.tensor(2.0, requires_grad=True)

Em seguida, configure as relações entre nossa entrada e cada camada de nossa rede neural, x, y e z. Observe que z é definido em termos de x e y, enquanto x e y são definidos usando nossos valores de entrada a e b.

import torch
# set up simple graph relating x, y and z
a = torch.tensor(3.0, requires_grad=True)
b = torch.tensor(2.0, requires_grad=True)

x = 2*a + 3*b
y = 5*a*a + 3*b*b*b
z = 2*x + 3*y

Isso cria uma cadeia de relacionamentos que o PyTorch pode seguir para entender todos os relacionamentos entre os dados.

Agora podemos calcular o gradiente dz/da​​ seguindo o caminho de volta de z para  a.

Existem dois caminhos, um passando por x e outro por y. Você deve seguir os dois e adicionar as expressões de ambos os caminhos. Isso faz sentido porque ambos os caminhos de a a z contribuem para o valor de z.

Teríamos encontrado o mesmo resultado se tivéssemos calculado dz/da usando a regra da cadeia do cálculo.

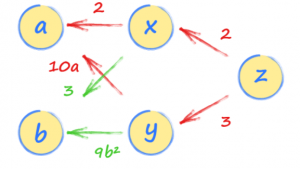
                                               Figura 04

O primeiro caminho por x nos dá 2 * 2 e o segundo caminho por y nos dá 3 * 10a. Assim, a taxa na qual z varia com a é 4 + 30a.

Se a é 22, então dz/da​​ é 4+30∗2=64.

Podemos confirmar isso no PyTorch adicionando uma propagação para trás de z e pedindo o gradiente (ou derivado) de a.

import torch
# set up simple graph relating x, y and z
a = torch.tensor(2.0, requires_grad=True)
b = torch.tensor(1.0, requires_grad=True)
x = 2*a + 3*b
y = 5*a*a + 3*b*b*b
z = 2*x + 3*y
print("a: ", a)
print("b: ", b)
print("x: ", x)
print("y: ", y)
print("z: ", z)
# work out gradients
z.backward()
print("Working out gradient dz/da")
# what is gradient at a = 2.0
print("Gradient at a=2.0:", a.grad)

Próximos passos para o seu aprendizado

Parabéns, você concluiu seu início rápido de PyTorch e Redes Neurais! A conclusão de um gráfico computacional é uma parte essencial da compreensão de redes de aprendizado profundo.

À medida que você aprender habilidades e aplicativos avançados de aprendizado profundo, você desejará explorar:

• Redes neurais complexas com otimização
• Design de visualização
• Treinamento com GANs

Vamos continuar aprendendo juntos!

Fonte: PyTorch tutorial: a quick guide for new learners